Question

Applying the formula for the sum of the first n integers? a-Evaluate 2+4+6+......+500​

Answer 1

`S_(250) = 62750`

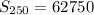
Step-by-step explanation:

Given

`Sequence: 2 + 4 + 6 + ..... + 500`

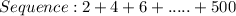
Required

Evaluate the sequence

The sequence shows an arithmetic progression and will be solved using the sum of n terms of an Arithmetic Sequence as follows:

`S_n = (n)/(2)(a + L)`

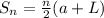
But first, we need to determine the value of n as follows:

`L = a + (n - 1)d`

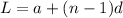
Where

`L = Last\ Term = 500`

`a = First\ Term = 2`

`d = Common\ Difference = 4 - 2 = 2`

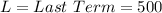
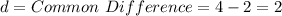
So:

`L = a + (n - 1)d`

`500 = 2 + (n - 1) * 2`

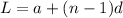
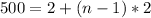
Open bracket

`500 = 2 + 2n - 2`

Collect Like Terms

`2n = 500 + 2 - 2`

`2n = 500`

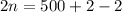
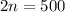
Divide through by 2

`n = 250`

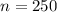
So:

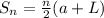`S_n = (n)/(2)(a + L)` becomes

`S_(250) = (250)/(2)(2 + 500)`

`S_(250) = 125(2 + 500)`

`S_(250) = 125(502)`

`S_(250) = 125 * 502`

`S_(250) = 62750`

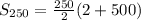
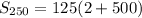
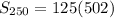
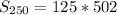
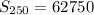
Hence, the sum of the sequence is 62750