Question

Calvin deposits $400 in a savings account that accrues 5% interest compounded monthly. After c years, Calvin has

$658.80. Makayla deposits $300 in a different savings account that accrues 6% interest compounded quarterly. After m
years, Makayla has $613.04. What is the in approximate difference in the number of years that Calvin and Makayla have
their money invested?
O Makayla invests her money 1 year longer.
O Makayla invests her money 2 years longer.
O Calvin invests his money 1 year longer.
O Calvin invests his money 2 years longer.

Answer 1

Dot number 2. Makayla invests her money 2 years longer.

Explanation:

Calvin 400$ with 5% interest compounded monthly will get you to 666.0294029241$ after 13 months or 1 year and 1 month

Makayla 300$ with 6% interest quarterly

1st year 378.743088$(4 quarters)

2nd year 478.1544223592$(+4 quarters)

3rd year 603.6589415506$(+4 quarters)

3rd year and 1 quarter 639.8784780436$

Answer 2

So the second option is the answer: Makayla invests her money 2 years longer.

Explanation:

Formula for compound interest:
`A=P(1+(r)/(n))^(nt)`

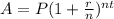
Calvin:

`A=658.80`

`P=400`

`r=0.05`

`n=12`

`t=?`

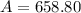
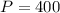
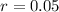
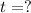
Makayla:

`A=613.04`

`P=300`

`r=0.06`

`n=4`

`t=?`

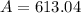
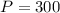
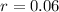
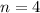
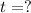
Lets solve for
`t`.

1) Divide both sides of the equation by
`P`.

`(A)/(P) =(1+(r)/(n))^(nt)`

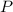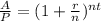
2) Take the natural log of both sides.

`ln((A)/(P)) =ln((1+(r)/(n))^(nt))`

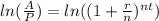
3) Rewrite the right side of the equation using properties of exponents.

`ln((A)/(P)) =nt*ln(1+(r)/(n))`

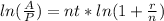
4) Divide each side of the equation by
`n*ln(1+(r)/(n))`

`\frac{nt*ln(1+\frac{r}n)}{n*ln(1+\frac{r}n)}=\frac{ln((A)/(P))}{n*ln(1+\frac{r}n)}`

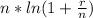
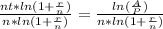
5) Cancel the common factor
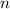`n` on the left side of the equation.

`\frac{t*ln(1+\frac{r}n)}{ln(1+\frac{r}n)}=\frac{ln((A)/(P))}{n*ln(1+\frac{r}n)}`

6) Cancel the common factor of
`ln(1+(r)/(n))`.

`t=(ln((A)/(P)))/(n*ln(1+(r)/(n)))`

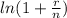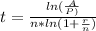
Now we have an equation for
`t` that we can use to answer your question.

For Calvin:

`t=(ln((658.80)/(400)))/(12*ln(1+(0.05)/(12)))`

`t=10`

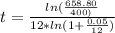
For Makayla:

`t=(ln((613.04)/(300)))/(3*ln(1+(0.06)/(3)))`

`t=12`

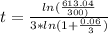
So the second option is the answer: Makayla invests her money 2 years longer.

Note: This question took me 2 minutes to answer but typing it took 30. lol