Answer:
Options (1) and (3)
Explanation:
Option (1)
f(x) = x²+ 3
We can rewrite the function in the equation form as,
y = x² + 3
By interchanging y by x,
x = y² + 3
Now we solve it for y,
y² = x - 3
y = ±√(x - 3)
So the inverse function is,
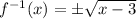
It's a function.
Option 2
d(x) = -9
Equation form of the function is,
y = -9
Replacing y by x,
x = - 9
Therefore, inverse function will be,
x = -9
Inverse is not a function
Option 3
m(x) = -7x
Equation form of the function,
y = -7x
Interchanging y by x,
x = -7y
Now solve for x,
y =
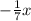
So the inverse function will be,
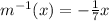
Inverse is a function.
Option 4
p(x) = |x|
As this function not a one to one function inverse function is not possible.
Inverse of |x| is not a function.