Question

Given an inequality, what strategies can we use to determine where the boundary line is? Explain your strategies in detail.

4x+3y≥12

Answer 1

Explanation:

The strategy to determine the boundary line is that we need to remove the inequality sign and replace it with and equal to sign and then sketch the equation of the function which is

`4x+3y=12`

to sketch the function we need the function's x-intercept which means the graphs crosses the x-axis at that specific point (x , 0) and y-intercept which means the graph crosses the y-axis at that specific point (0 , y).

Since both these points lie on line we can substitute it into the equation to find the x-y intercepts and hence sketch the line so here goes.

For x-intercept:

`4x+3y=12\\4(x)+3(0)=12\\4x=12\\x=12/4\\x=3`

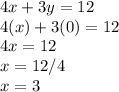
so the x-intercept is (3 , 0)

For y-intercept:

`4x+3y=12\\4(0)+3(y)=12\\3y=12\\y=12/3\\y=4`

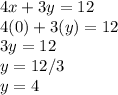
so the y-intercept is (0 , 4)

now we sketch these 2 points and draw a straight line joining both the points as shown in the image below.