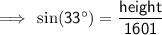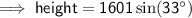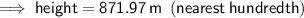Question

Please and Thank you!

A meteorologist measures the angle of elevation to her weather balloon as 33 degrees. A radio signal from the balloon indicates that it is 1601 meters diagonally from her location. How high is the weather balloon above the ground? Round to the nearest hundredth.
A. 871.97 feet
B. 1342.71 feet
C. 2939.56 feet
D. 1039.70 feet

Answer 1

Use sine

• sin33=Perpendicular/Hypotenuse
• sin33=P/1601
• P=1601sin33
• P=871.97ft

Answer 2

A. 871.97 m

Explanation:

Model this is a right triangle.

Use the sine trigonometric ratio to find the height of the weather balloon from the ground.

Sine trigonometric ratio

`\sf \sin(\theta)=(O)/(H)`

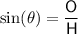
where:

• 
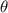  `\theta` is the angle
• O is the side opposite the angle
• H is the hypotenuse (the side opposite the right angle)

Given:

• 
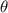  `\theta` = 33°
• O = height
• H = 1601 m

Substitute the given values into the formula and solve for O:

`\implies \sf \sin(33^(\circ))=(height)/(1601)`

`\implies \sf height=1601\sin(33^(\circ))`

`\implies \sf height=871.97\:m\:\:(nearest\:hundredth)`