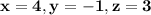Question

What is the solution to the following system x+y+z=6 and x-y+z=8 and x+y-z=0

Answer 1

`\boxed{x = 4, ~y = -1,~ and~z = 3}`

.

Explanation:

(eq-1) → x + y + z = 6

(eq-2) → x - y + z = 8

(eq-3) → x + y - z = 0

.

Eliminate eq-1 and eq-3

`x + y + z = 6`

x + y - z = 0

`2z = 6`

`z = (6)/(2)`

`z = 3`

.

Eliminate eq-1 and qe-2

`x + y + z = 6`

x - y + z = 8

`2y = -2`

`y = (-2)/(2)`

`y = -1`

.

Substitute the value of z and y to on of equations

`x + y + z = 6`

`x + (-1) + 3 = 6`

`x + 2 = 6`

`x = 6 - 2`

`x = 4`

Answer 2

The solution for the following system is:
`\mathbf{x=4, y=-1, z=3}`

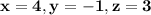
Explanation:

We need to find the solution to the following system.

`x+y+z=6 \ and \ x-y+z=8 \ and \ x+y-z=0`

Let:

`x+y+z=6 --eq(1)\\ x-y+z=8 --eq(2)\\ x+y-z=0--eq(3)`

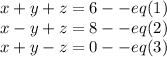
Adding eq(1) and eq(2)

`x+y+z=6 \\x-y+z=8 \\-------\\2x+2z=14 --eq(4)`

Adding eq(2) and eq(3)

`x-y+z=8 \\ x+y-z=0\\-------\\2x=8\\x=8/2\\x=4`

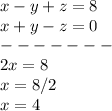
We get value of x=4

Now, putting value of x in eq(4) to find value of z

`2x+2z=14\\Put x=4\\2(4)+2z=14\\8+2z=14\\2z=14-8\\2z=6\\z=6/2\\z=3`

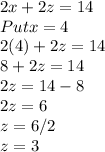
We get value of z=3

Now, putting value of x and z in eq(1) to find value of y

`x+y+z=6\\Put \ x=4, z=3\\4+y+3=6\\y+7=6\\y=6-7\\y=-1`

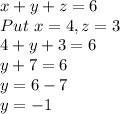
So, value of y=-1

The solution for the following system is:
`\mathbf{x=4, y=-1, z=3}`