The GCD is
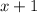 , so
, so
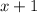 divides both
divides both
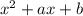 and
and
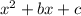 . For some
. For some
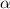 and
and
 we can write
we can write


Expanding the right sides, we get
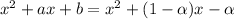
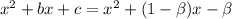
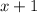 also divides the LCM, so
also divides the LCM, so
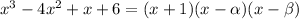
and expanding gives
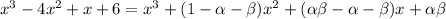
Matching up all the coefficients, we have
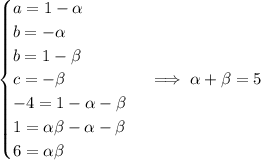
All the unknowns are integers, and we have the prime factorization 6 = 2×3 that also satisfies 5 = 2 + 3.
• If
 and
and
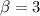 , then
, then
 ,
,
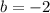 , and
, and
 .
.
• If
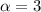 and
and
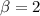 , then there is no solution for
, then there is no solution for
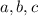 since
since

but 3 ≠ 2 - 1 = 1.
It follows that
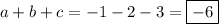 .
.