Question

Avery has $760 to spend at a bicycle store for some new gear and biking outfits. Assume all prices listed include tax. She buys a new bicycle for $239.70. She buys 3 bicycle reflectors for $18.63 each and a pair of bike gloves for $30.79. She plans to spend some or all of the money she has left to buy new biking outfits for $78.84 each. Write and solve an inequality which can be used to determine xx, the number of outfits Avery can purchase while staying within her budget.

Answer 1

Not more than 5 outfits

Explanation:

Given

`Total = \$760`

`New\ Bicycle = \$239.70`

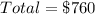
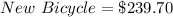
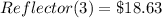`Reflector (3) = \$18.63` (each)

`Glove = \$30.79`

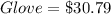
First, we calculate the amount left.

`Amount = Total - (New\ Bicycle + Reflector * 3 + Glove)`

`Amount = \$760 - (\$239.70 + \$18.63 * 3 + \$30.79)`

`Amount = \$760 - (\$239.70 + \$55.89 + \$30.79)`

`Amount = \$760 - (\$326.38)`

`Amount = \$760 - \$326.38`

`Amount = \$433.62`

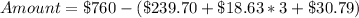
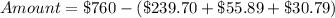
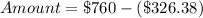
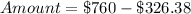
An outfit costs $78.84 and he plans to buy x outfits.

The inequality is represented as follows:

`\$78.84 * x \leq \$433.62`

i.e. the amount to spend on outfits can't exceed $433.62

Divide both sides by $78.84

`(\$78.84 * x)/(\$78.84) \leq (\$433.62)/(\$78.84)`

`x \leq (\$433.62)/(\$78.84)`

`x \leq (433.62)/(78.84)`

`x \leq 5.5`

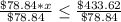
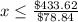
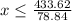
Since there is no 0.5 outfit, then She can only afford a maximum of 5 outfits to stay within budget.