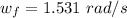Answer:
The angular velocity is
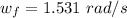
Step-by-step explanation:
From the question we are told that
The mass of each astronauts is
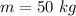
The initial distance between the two astronauts
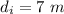
Generally the radius is mathematically represented as
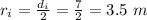
The initial angular velocity is
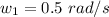
The distance between the two astronauts after the rope is pulled is

Generally the radius is mathematically represented as
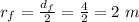
Generally from the law of angular momentum conservation we have that

Here
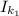 is the initial moment of inertia of the first astronauts which is equal to
is the initial moment of inertia of the first astronauts which is equal to
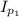 the initial moment of inertia of the second astronauts So
the initial moment of inertia of the second astronauts So
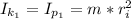
Also
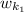 is the initial angular velocity of the first astronauts which is equal to
is the initial angular velocity of the first astronauts which is equal to
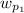 the initial angular velocity of the second astronauts So
the initial angular velocity of the second astronauts So
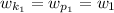
Here
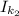 is the final moment of inertia of the first astronauts which is equal to
is the final moment of inertia of the first astronauts which is equal to
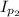 the final moment of inertia of the second astronauts So
the final moment of inertia of the second astronauts So
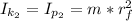
Also
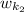 is the final angular velocity of the first astronauts which is equal to
is the final angular velocity of the first astronauts which is equal to
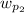 the final angular velocity of the second astronauts So
the final angular velocity of the second astronauts So
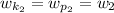
So
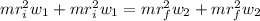
=>
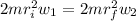
=>
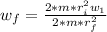
=>
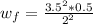
=>