Answer:
Explanation:
Given that:
The number of observations (n) = 28
The mean
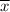 is the addition of all the given numbers divided by the total number of observations = 64.76/28
is the addition of all the given numbers divided by the total number of observations = 64.76/28
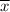 = 2.31
= 2.31
The standard deviation s = 0.65
At 68%; the empirical rule falls between:
=

= 2.31 ± 0,65
= ( 2.31 - 0.65, 2.31 + 0.65)
= (1.66 , 2.96)
From the parameters given:
4 values are < 1.66 and 6 values are > 2.96
Thus, the percentage covered = (28 - (6+4))/28 × 100
= (28 - 10) / 28 × 100
= (18/28) × 100
= 64.29%
Hence, this satisfies the normal distribution
At 95; the empirical rule falls between:
=

= 2.31 ± 2(0.65)
= 2.31 ± 1.30
= ( 2.31 - 1.30, 2.31 + 1.30)
= (1.01 , 3.61)
From the parameters given:
0 values are < 1.01 and 1 values are > 3.61
Thus, the percentage covered = (28 - (1+0))/28 × 100
= (28 - 1) / 28 × 100
= (27/28) × 100
= 96.43%
Hence, this satisfies the normal distribution
At 99.7; the empirical rule falls between:
=
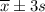
= 2.31 ± 3(0.65)
= 2.31 ± 1.95
= ( 2.31 - 1.95, 2.31 + 1.95)
= (0.36 , 4.26)
From the parameters given:
0 values are < 0.36 and 0 values are > 4.26
Thus, the percentage covered = (28 - (0+0))/28 × 100
= (28 - 0) / 28 × 100
= (28/28) × 100
=100%
Hence, this satisfies the normal distribution and the maximum daily rainfall totals could be considered to be normally distributed.