Question

Can someone please help me with The Questions #14 and #15 of The Operations On The Polynomials & The Special Products for me, please guys? :)

Answer 1

Formulas

`\textsf{Area of a circle}=\pi r^2 \quad \textsf{(where r is the radius)}`

`\textsf{Radius of a circle}=(1)/(2)d \quad \textsf{(where d is the diameter)}`

`\textsf{Area of a square}=s^2 \quad \textsf{(where s is the side length)}`

`\textsf{Diagonal of a square}=s√(2) \quad \textsf{(where s is the side length)}`

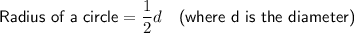
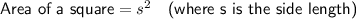
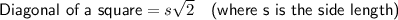
Question 14

If a circle is inscribed in a square, then the diameter of the circle is equal to the side length of the square. Therefore, as the radius of a circle is half the diameter, the radius of the circle is half the side length of the square.

Given:

• 
  `s= 12x\:\: \sf cm`

• 
  `r=(1)/(2)s=6x\:\: \sf cm`

Therefore, the areas of the square and circle are:

`\begin{aligned} \textsf{Area of the circle} & =\pi (6x)^2\\ & = 36 \pi x^2 \:\: \sf cm^2 \end{aligned}`

`\begin{aligned}\textsf{Area of the square}& =(12x)^2\\ & = 144x^2 \:\: \sf cm^2 \end{aligned}`

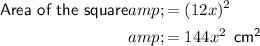
Therefore, the ratio of the circle to square is:

`\implies \sf circle : square`

`\implies 36 \pi x^2:144x^2`

`\implies 36 \pi :144`

`\implies \pi : 4`

`\implies (1)/(4) \pi : 1`

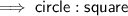
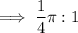
So the circle is ¹/₄π the size of the square.

Question 15

If a square is inscribed in a circle, then the diagonal of the square is the diameter of the circle. Therefore, as the radius of a circle is half the diameter, the radius of the circle is half the diagonal of the square.

Given:

• 
  `r = 5a^2 \:\: \sf cm`

• 
  `d=2r=10a^2 \:\: \sf cm`

`\begin{aligned} \textsf{Area of the circle} & =\pi (5a^2)^2\\ & = 25 \pi a^4 \:\: \sf cm^2 \end{aligned}`

`\begin{aligned}\textsf{Diagonal of a square} & =s√(2)\\10a^2 & = s √(2)\\ s & =(10a^2)/(√(2))\\ s & = 5√(2)a^2\:\: \sf cm^ \end{aligned}`

`\begin{aligned}\textsf{Area of the square}& =(5√(2)a^2)^2\\ & = 50a^4 \:\: \sf cm^2 \end{aligned}`

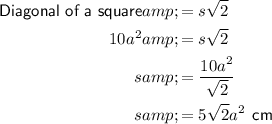
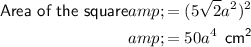
Therefore, the ratio of the circle to square is:

`\implies \sf circle : square`

`\implies 25 \pi a^4:50a^4`

`\implies 25 \pi :50`

`\implies \pi : 2`

`\implies (1)/(2) \pi:1`

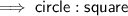
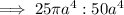
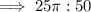
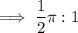
So the circle is ¹/₂π the size of the square.