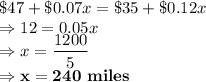Question

You want to rent a car for the day.Prestige car rentals charges $47 plus $0.07 per mile to rent a midsize vehicle . Gateway Auto changes a $35 fee plus $0.12 per mile for the same car. For what number of miles will both companies charge the same price?

Answer 1

240 miles

Explanation:

Given that:

Charges offered by Prestige car rentals for renting a midsize vehicle:

Fixed charges = $47

Per mile charges for renting a midsize vehicle = $0.07

Charges offered by Gateway Auto for renting a midsize vehicle:

Fixed charges = $35

Per mile charges for renting a midsize vehicle = $0.12

To find:

Number of miles for which both the companies charge the same price?

Solution:

Let the number of miles for which both the companies will charge the same price =
`x` miles

Charges for one mile by Prestige car rentals = $0.07

Charges for
`x` miles by Prestige car rentals = $0.07
`x`

Total charges by Prestige Car rentals = $47 + $0.07
`x`

Charges for one mile by Gateway Auto = $0.12

Charges for
`x` miles by Gateway Auto = $0.12
`x`

Total charges by Gateway Auto = $35 + $0.12
`x`

As per question statement, the charges are same:

`\$47 + \$0.07x = \$35 + \$0.12x\\\Rightarrow 12=0.05x\\\Rightarrow x=(1200)/(5)\\\Rightarrow \bold{x=240\ miles}`