Question

Bro why cant I post this T-T

Answer 1

Answer: 12.0 m/s^2

Step-by-step explanation:

Let
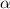`\alpha` be the angular acceleration of the end of the rod

Taking torque about the link, we have:

`\tau = W * OM\\ or\\ \tau = mg* \left((L)/(2)\right)\sin 55^\circ ....(i)`

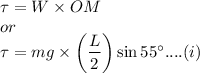
Torque is also given in terms of moment of inertia of the rod and its angular acceleration i.e.

`\tau = I_(rod)\ \alpha......(ii)`

From equations (i) and (ii) we have:

`mg* \left((L)/(2)\right)\sin 55^\circ = \left((mL^2)/(3)\right)\alpha\ \ \ \ \ \ \ (\because I_(rod) = (mL^2)/(3)) \\ \\ \alpha = \left((3g)/(2L)\right)\sin 55^\circ\\ \\ \alpha = \left((3* 9.8)/(2* 2.4)\right)\sin 55^\circ\\ \\ \boxed{\alpha = 5.02\ rad/s^2} }`

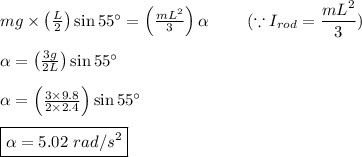
The acceleration of the end of the rod farthest from the link is given by:

`a = L\alpha\\ \\ a = (2.4\ m)(5.02\ rad/s^2)\\ \\ \boxed{a = 12.0\ m/s^2}`