Answer:

Explanation:
To find the perimeter, you must first find the side length.
We are given the area. The formula for the area of a square is:
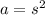
We know the room's area is 196 square feet.
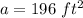
Substitute the area in.

We want to find the side length, so we must isolate s on one side of the equation.
- s is being squared.
- The inverse of a square is the square root.
- Take the square root of both sides of the equation.
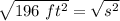

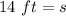
Now, find the perimeter. This can be found using:

We know the side length is 14 feet.
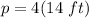
Multiply.

The perimeter of the room is 14 feet.