Question

-4(x + 3) <-2 – 2x?
What’s the answer on the number line for this equation

Answer 1

`x>-5`

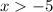
The solution graph is also attached below. On the solution graph, the value will be:

Explanation:

Given the expression

`-4\left(x\:+\:3\right)\:<\:-2\:-\:2x`

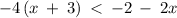
Expanding

`-4x-12<-2-2x`

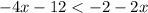
Add 12 to both sides

`-4x-12+12<-2-2x+12`

`-4x<-2x+10`

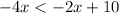
Add 2x to both sides

`-4x+2x<-2x+10+2x`

`-2x<10`

`\mathrm{Multiply\:both\:sides\:by\:-1\:\left(reverse\:the\:inequality\right)}`

`\left(-2x\right)\left(-1\right)>10\left(-1\right)`

`2x>-10`

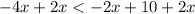
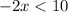
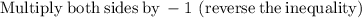
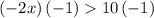
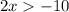
Divide both sides by 2

`(2x)/(2)>(-10)/(2)`

`x>-5`

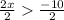
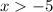
The solution graph is also attached below. On the solution graph, the value will be:

• 
  `x>-5`